Video: Mengapa identitas trigonometri berguna dalam menyelesaikan persamaan?
2024 Pengarang: Lynn Donovan | [email protected]. Terakhir diubah: 2023-12-15 23:48
Identitas memungkinkan kita untuk menyederhanakan ekspresi yang rumit. Mereka adalah alat dasar dari trigonometri yang digunakan dalam menyelesaikan persamaan trigonometri , seperti halnya memfaktorkan, menemukan penyebut yang sama, dan menggunakan rumus khusus adalah alat dasar dari memecahkan aljabar persamaan.
Lalu, apa yang membuat persamaan trigonometri menjadi identitas?
Dalam matematika, identitas trigonometri adalah persamaan yang melibatkan trigonometri fungsi dan benar untuk setiap nilai dari variabel yang terjadi di mana kedua sisi persamaan didefinisikan. Secara geometris, ini adalah identitas melibatkan fungsi tertentu dari satu atau lebih sudut.
Juga Tahu, apa persamaan trigonometri? A persamaan trigonometri apakah ada? persamaan yang mengandung trigonometri fungsi. Seperti yang disebutkan dalam trigonometri Identitas, persamaan trigonometri yang berlaku untuk setiap sudut disebut a trigonometri identitas. Ada yang lain persamaan , meskipun, itu hanya berlaku untuk sudut tertentu.
Demikian pula orang mungkin bertanya, apa cara termudah untuk menyelesaikan identitas trigonometri?
LANGKAH 1: Ubah semua sec, csc, cot, dan tan menjadi sin dan cos. Sebagian besar ini dapat dilakukan dengan menggunakan hasil bagi dan timbal balik identitas . LANGKAH 2: Periksa semua sudut untuk jumlah dan perbedaan dan gunakan yang sesuai identitas untuk menghapusnya. LANGKAH 3: Periksa kelipatan sudut dan hapus dengan menggunakan rumus yang sesuai.
Apa yang sama dengan dosa 2x?
sin2x =( dosa x)2=12(1−cos( 2x )).
Direkomendasikan:
Mengapa diagram kasus berguna?
Saat menggunakan Unified Modeling Language (UML), diagram kasus penggunaan membantu Anda memahami bagaimana pengguna dapat berinteraksi dengan sistem yang telah Anda rekayasa. Dan pada akhirnya, ini akan membantu tim Anda menentukan dan mengatur persyaratan. Sebaliknya, mereka mewakili gambaran umum tingkat tinggi tentang bagaimana kasus penggunaan, aktor, dan sistem Anda berhubungan
Mengapa dioda Schottky berguna untuk penyearah frekuensi tinggi?
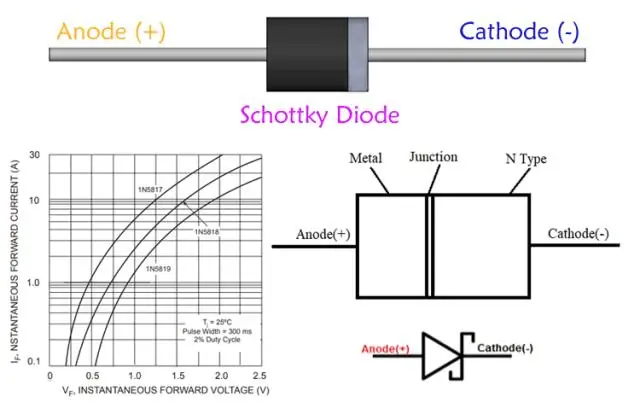
Aplikasi dioda Schottky. Penyearah Daya: Dioda Schottky juga digunakan sebagai penyearah daya tinggi. Kepadatan arusnya yang tinggi dan penurunan tegangan maju yang rendah berarti bahwa lebih sedikit daya yang terbuang daripada dioda sambungan PN biasa yang digunakan. Schottkydiode cenderung memiliki arus bocor terbalik yang tinggi
Mengapa heksadesimal adalah sistem penomoran yang berguna?
Sistem heksadesimal biasanya digunakan oleh pemrogram untuk menggambarkan lokasi dalam memori karena dapat mewakili setiap byte (yaitu, delapan bit) sebagai dua digit heksadesimal berturut-turut, bukan delapan digit yang akan dibutuhkan oleh bilangan biner (yaitu, basis 2) dan tiga digit yang akan diperlukan dengan desimal
Mengapa generator berguna?
Generator telah menjadi bagian penting dari Python sejak diperkenalkan dengan PEP 255. Fungsi generator memungkinkan Anda untuk mendeklarasikan fungsi yang berperilaku seperti iterator. Mereka memungkinkan pemrogram untuk membuat iterator dengan cara yang cepat, mudah, dan bersih. Iterator adalah objek yang dapat diulang (diulang) pada
Bagaimana cara menyelesaikan persamaan di Mathcad?
Menyelesaikan Persamaan Secara Simbolis. Ketik persamaan yang akan diselesaikan menggunakan Boolean sama dengan operator. Masukkan operator evaluasi simbolis, ketik penyelesaian kata kunci di placeholder, lalu tekan Enter atau klik di mana saja. PTC Mathcad mengembalikan solusi simbolis ke persamaan, jika memungkinkan